Cara Paling Gampang Menyederhanakan Belahan + Pola Soal Dan Pembahasan (Materi Smp)

Dalam artikel sebelumnya telah dijelaskan bahwa pecahan merupakan bilangan yang sanggup dinyatakan dalam bentuk “a/b”, dengan a dan b yaitu bilangan bulat, b ≠ 0, dan b bukan faktor dari a. Bilangan a disebut pembilang, b disebut penyebut. Nah, pada kesempatan kali ini kita akan berguru mengenai cara menyederhanakan potongan beserta teladan soal dan pembahasannya.

Suatu potongan yang telah mengalami penyederhanaan akan menjadi potongan sederhana. Lalu tahukah kalian apa yang dimaksud dengan potongan sederhana itu? Untuk mengetahui jawabannya, silahkan kalian simak baik-baik klarifikasi berikut ini. Selamat berguru dan semoga sanggup paham.

Perhatikan bab yang diarsir dari gambar-gambar di atas dan pecahan-pecahan yang melambangkannya. Ada berapa bab pada masing-masing gambar? Ada berapa bab yang diarsir? Bilangan potongan manakah yang melambangkan bab yang di arsir? Pecahan yang melambangkan bab yang diarsir dari kotak paling kiri hingga paling kanan berturut-turut adalah 1/2, 2/4, 3/6, dan 4/8.

Pecahan 1/2, 2/4, 3/6, dan 4/8 mewakili kawasan yang sama besar, alasannya yaitu itu disebut pecahan-pecahan senilai. Dari empat potongan tersebut, 1/2 merupakan dengan bentuk paling sederhana. Suatu potongan dikatakan dalam bentuk paling sederhana (pecahan sederhana) kalau faktor komplotan terbesar (FPB) dari pembilangan dan penyebutnya yaitu 1.

Kalian sanggup menulis bentuk paling sederhana dari suatu potongan dengan cara membagi pembilang dan penyebut potongan itu dengan FPB dari pembilangan dan penyebutnya.

Contoh:

Tulislah 20/28 dalam bentuk paling sederhana.

Penyelesaian:

Langkah pertama yaitu memilih FPB dari pembilangan dan penyebut potongan tersebut yaitu bilangan 20 dan 28. Masih ingatkah kalian cara memilih KPK dan FPB suatu bilangan bulat? Ya, benar sekali. Langkah paling gampang dan simpel untuk memilih KPK dan FPB dua bilangan atau lebih yaitu dengan mencari faktorisasi prima dari bilangan-bilangan yang bersangkutan.

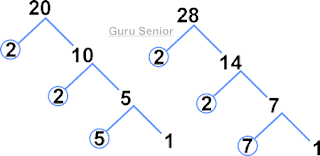
Faktorisasi prima suatu bilangan sanggup diketahui dengan memakai pohon faktor. Berikut ini yaitu pohon faktor dari bilangan 20 dan 28.

Dari gambar pohon faktor di atas, maka faktorisasi prima dari 20 dan 28 yaitu sebagai berikut.

20 = 22 × 5

28 = 22 × 7

Bilangan terkecil dengan pangkat terkecil yang merupakan faktor prima dari 20 dan 28 yaitu 22 = 4. Makara FPB dari bilangan 20 dan 28 yaitu 4. Dengan demikian, pecahan 20/28 dapat kita sederhanakan dengan cara berikut.

20 : 4	=	5
28 : 4		7

Jadi, bentuk paling sederhana dari pecahan 20/28 adalah 5/7.

Sekarang supaya kalian lebih paham mengenai cara menyederhanakan pecahan, silahkan kalian pelajari beberapa teladan soal dan pembahasannya berikut ini.

Contoh Soal 1:

Sederhanakanlah bentuk pecahan 77/80

Penyelesaian:

Pertama kita tentukan dahulu faktorisasi prima dari pembilang dan penyebutnya yaitu 77 dan 80. Perhatikan pohon faktor berikut ini.

Dari gambar pohon faktor tersebut, maka faktorisasi prima dari 77 dan 80 yaitu sebagai berikut,

77 = 7 × 11

80 = 24 × 5

Karena kedua bilangan tersebut tidak mempunyai faktor prima yang sama, maka FPB dari 77 dan 80 yaitu 1. Jadi, pecahan 77/80 adalah bentuk potongan yang paling sederhana.

Contoh Soal 2:

Tulislah 120/260 dalam bentuk paling sederhana.

Penyelesaian:

Seperti pada langkah sebelumnya, kita tentukan FPB dari 120 dan 260 dengan menguraikan faktorisasi prima kedua bilangan tersebut. Perhatikan pohon faktor berikut ini.

Berdasarkan pohon faktor tersebut, maka faktorisasi prima dari bilangan 120 dan 260 yaitu sebagai berikut.

120 = 23 × 3 × 5

260 = 22 × 5 × 13

Bilangan terkecil dengan pangkat terkecil yang merupakan faktor prima dari 120 dan 260 yaitu 22 dan 5. Makara FPB dari bilangan 120 dan 260 yaitu 22 ×5 = 20. Dengan demikian, pecahan 120/260 dapat kita sederhanakan dengan cara berikut.

120 : 20	=	6
260 : 20		13

Jadi, bentuk paling sederhana dari pecahan 120/260 adalah 6/13.

Contoh Soal 3:

Tulislah 240/320 dalam bentuk paling sederhana.

Penyelesaian:

Sekarang kita akan coba memakai teknik lain selain memilih FPB pembilang dan penyebutnya terlebih dahulu. Langkah pertama yaitu membagi bilangan 240 dan 320 dengan bilangan paling besar yang masih sanggup kalian jangkau operasi hitungnya. Karena kedua bilangan tersebut berakhiran 0 (nol), maka niscaya sanggup dibagi dengan 10. Oleh alasannya yaitu itu, kita bagi 240 dan 320 dengan 10, sehingga alhasil yaitu sebagai berikut.

240 : 10	=	24
320 : 10		32

Sekarang coba kalian perhatikan pembilang dan penyebut potongan tersebut. Apakah 24 dan 32 masih sanggup kita bagi dengan bilangan yang sama? Tentu saja bisa. Misalkan kita bagi dengan 4, maka alhasil yaitu sebagai berikut.

24 : 4	=	6
32 : 4		8

Sekarang kita dapatkan pecahan 6/8. Apakah pembilang dan penyebut potongan ini masih sanggup kita bagi lagi dengan bilangan bulat yang sama? Tentu masih bisa, yaitu dibagi dengan angka 2, sehingga alhasil yaitu sebagai berikut.

6 : 2	=	3
8 : 2		4

Nah, hingga disini kita peroleh pecahan 3/4. Pecahan bentuk ini merupakan yang paling sederhana alasannya yaitu sudah tidak sanggup dibagi lagi dengan bilangan yang sama yang lebih besar dari 1. Dengan demikian, bentuk sederhana dari pecahan 240/320 adalah 3/4.