Perlu kalian ingat bahwa pada perkalian bilangan lingkaran berlaku sifat distributif perkalian terhadap penjumlahan, yaitu a × (b + c) = (a × b) + (a × c) dan sifat distributif perkalian terhadap pengurangan, yaitu a × (b – c) = (a × b) – (a × c), untuk setiap bilangan lingkaran a, b, dan c. Sifat ini juga berlaku pada perkalian bentuk aljabar.
1. Perkalian antara konstanta dengan bentuk aljabar
Perkalian suatu bilangan konstanta k dengan bentuk aljabar suku satu dan suku dua dinyatakan sebagai berikut.
k(ax) = kax k(ax + b) = kax + kb |
Contoh:
Jabarkan bentuk aljabar berikut ini, lalu sederhanakanlah.
a. 4(p + q)
b. 5(ax + by)
c. 3(x – 2) + 6(7x + 1)
d. -8(2x – y + 3z)
Penyelesaian:
a. 4(p + q) = 4p + 4q
b. 5(ax + by) = 5ax + 5by
c. 3(x – 2) + 6(7x + 1) = 3x – 6 + 42x + 6
= 3x + 42x – 6 + 6
= (3 + 42)x + 0
= 45x
d. -8(2x – y + 3z) = -16x + 8y – 24z
Soal Tantangan |
Panjang sisi miring segitiga siku-siku yaitu (2x + 1) cm, sedangkan panjang sisi siku-sikunya (3x – 2) cm dan (4x – 5) cm. Tentukan luas segitiga tersebut. |
2. Perkalian antara dua bentuk aljabar
Sebagaimana perkalian suatu konstanta dengan bentuk aljabar, untuk memilih hasil kali antara dua bentuk aljabar kita sanggup memanfaatkan sifat distributif perkalian terhadap penjumlahan dan sifat distributif perkalian terhadap pengurangan.
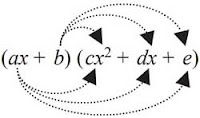
Selain dengan cara tersebut, untuk memilih hasil kali antara dua bentuk aljabar, sanggup memakai cara sebagai berikut. Perhatikan perkalian antara bentuk aljabar suku dua dengan suku dua berikut.
Selain dengan cara sketsa menyerupai di atas, untuk mengalikan bentuk aljabar suku dua dengan suku dua sanggup dipakai sifat distributif menyerupai uraian berikut ini.
(ax + b)(cx + d) = ax(cx + d) + b(cx + d)
= ax × cx + ax × d + b × cx + b × d
= acx2 + adx + bcx + bd
= acx2 + (ad + bc)x + bd
Berfikir Kritis |
Diskusikan dengan temanmu. Dengan memanfaatkan sifat distributif perkalian terhadap penjumlahan dan sifat distributif perkalian terhadap pengurangan, buktikan perkalian bentuk aljabar berikut. (ax + b)(ax – b) = a2x2 – b2(ax + b)2 = a2x2 + 2abx + b2(ax – b)2 = a2x2 – 2abx + b2 |
Adapun pada perkalian bentuk aljabar suku dua dengan suku tiga berlaku sebagai berikut.
= ax × cx2 + ax × dx + ax × e + b × cx2 + b × dx + b × e
= acx3 + adx2 + aex + bcx2 + bdx + be
= acx3 + (ad + bc)x2 + (ae + bd)x + be
Berfikir Kritis |
Coba jabarkan perkalian bentuk aljabar (ax + b)(cx2 + dx + e) dengan memakai sifat distributif. Bandingkan kesannya dengan uraian di atas. |
Contoh:
Tentukan hasil perkalian bentuk aljabar berikut dalam bentuk jumlah atau selisih.
1. (2x + 3)(3x – 2)
2. (–4a + b)(4a + 2b)
3. (2x – 1)(x2 – 2x + 4)
4. (x + 2)(x – 2)
Penyelesaian:
1. (2x + 3)(3x – 2) kita selesaian dengan dua cara, yaitu sebagai berikut.
● Cara (1) dengan sifat distributif
(2x + 3)(3x – 2) = 2x(3x – 2) + 3(3x – 2)
= 6x2 – 4x + 9x – 6
= 6x2 + 5x – 6
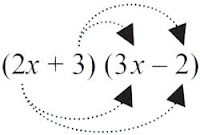
● Cara (2) dengan skema
= 2x × 3x + 2x × (–2) + 3 × 3x + 3 × (–2)
= 6x2 – 4x + 9x – 6
= 6x2 + 5x – 6
2. (–4a + b)(4a + 2b) kita selesaikan dengan dua cara, yaitu sebagai berikut.
● Cara (1) dengan sifat distributif
(–4a + b)(4a + 2b) = –4a(4a + 2b) + b(4a + 2b)
= –16a2 – 8ab + 4ab + 2b2
= –16a2 – 4ab + 2b2
● Cara (2) dengan skema
= (–4a) × 4a + (–4a) × 2b + b × 4a + b × 2b
= –16a2 – 8ab + 4ab + 2b2
= –16a2 – 4ab + 2b2
3. (2x – 1)(x2 – 2x + 4) kita selesaikan dengan dua cara, yaitu sebagai berikut.
● Cara (1) dengan sifat distributif
(2x – 1) (x2 – 2x + 4) = 2x(x2 – 2x + 4) – 1(x2 – 2x + 4)
= 2x3 – 4x2 + 8x – x2 + 2x – 4
= 2x3 – 4x2 – x2 + 8x + 2x – 4
= 2x3 – 5x2 + 10x – 4
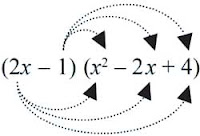
● Cara (2) dengan skema
= 2x × x2 + 2x × (–2x) + 2x × 4 + (–1) × x2 + (– 1) × (–2x) + (–1) × 4
= 2x3 – 4x2 + 8x – x2 + 2x – 4
= 2x3 – 4x2 – x2 + 8x + 2x – 4
= 2x3 – 5x2 + 10x – 4
4. (x + 2)(x – 2) kita selesaikan dengan dua cara, yaitu sebagai berikut.
● Cara (1) dengan sifat distributif
(x + 2)(x – 2) = x(x – 2) + 2(x – 2)
= x2 – 2x + 2x – 4
= x2 – 4
● Cara (2) dengan skema
= x × x + x × (–2) + 2 × x + 2 × (–2)
= x2 – 2x + 2x – 4
= x2 – 4
Menyatakan bentuk perkalian menjadi bentuk penjumlahan menyerupai tersebut di atas disebut menjabarkan atau menguraikan. Amatilah referensi soal nomor 4 di atas. Apakah kalian setuju bahwa secara umum bentuk perkalian (x + a)(x – a) = x2 – a2? Diskusikan hal tersebut dengan temanmu.
Kumpulan Contoh Soal dan Pembahasan
1. Sederhanakanlah bentuk-bentuk aljabar berikut ini.
a. 2(–8a – 3b) –4a + 9b
b. –3(4k2l + 3kl2) + 2(–9k2l – 4kl2)
c. 5(3m3 – 5m2 + m) – 2(m3 + 4m2 – 9m)
Penyelesaian:
a. 2(–8a – 3b) – 4a + 9b = -16a – 6b – 4a + 9b
= -16a – 4a – 6b + 9b
= (-16 – 4)a + (-6 + 9)b
= -20a + 3b
b. –3(4k2l + 3kl2) + 2(–9k2l – 4kl2)
= –12k2l – 9kl2 – 18k2l – 8kl2
= –12k2l – 18k2l – 9kl2 – 8kl2
= (-12 – 18)k2l + (-9 – 8)kl2
= -30k2l – 17kl2
c. 5(3m3 – 5m2 + m) – 2(m3 + 4m2 – 9m)
= 15m3 – 25m2 + 5m – 2m3 – 8m2 + 18m
= 15m3 – 2m3 – 25m2 – 8m2 + 5m + 18m
= (15 – 2)m3 + (-25 – 8)m2 + (5 + 18)m
= 13m3 – 33m2 + 23m
2. Nyatakan hasil perkalian bentuk aljabar berikut sebagai jumlah atau selisih.
a. -3(a – 2b + 5)
b. xy(x2 – 4)
c. 1/2(2x + 6)
d. 2(x + 3)
e. -3(2a + 5)
f. –p(p2 – 3)
Penyelesaian:
a. -3(a – 2b + 5) = -3a + 6b – 15
b. xy(x2 – 4) = x3y – 4xy
c. 1/2(2x + 6) = x + 3
d. 2(x + 3) = 2x + 6
e. -3(2a + 5) = -6a – 15
f. –p(p2 – 3) = -p3 + 3p
3. Nyatakan bentuk aljabar berikut sebagai perkalian konstanta dengan bentuk aljabar.
a. 5x – 15y
b. –2p + q – 3r
c. 3x2 + 9xy – 18xy2
d. –4p + 8r2
Penyelesaian:
a. 5x – 15y
konstanta-konstantanya yaitu 5 dan -15. FPB dari 5 dan 15 yaitu 5, maka bentuk perkalian konstantanya yaitu sebagai berikut.
5x – 15y = 5(x – 3y)
b. –2p + q – 3r
konstanta-konstantanya adalah-2, 1 dan -3. FPB-nya sudah niscaya 1, maka bentuk aljabar tersebut tidak sanggup dinyatakan sebagai perkalian konstanta.
c. 3x2 + 9xy – 18xy2
konstanta-konstantanya yaitu 3, 9, dan -18. FPB dari bilangan-bilangan 3, 9 dan 18 yaitu 3. Maka bentuk perkalian kontantanya yaitu sebagai berikut.
3x2 + 9xy – 18xy2 = 3(x2 + 3xy – 6xy2)
d. –4p + 8r2
konstanta-konstantanya yaitu -4 dan 8. FPB dari 4 dan 8 yaitu 4. Dengan demikian, bentuk perkalian konstantanya yaitu sebagai berikut.
–4p + 8r2 = 4(-p + 2r2)
Atau sanggup juga dituliskan sebagai berikut.
–4p + 8r2 = -4(p – 2r2)
4. Tentukan hasil pembagian terstruktur mengenai bentuk aljabar berikut ini.
a. (x + 2)(x – 3)
b. (2x – 3)(x + 4)
c. (4k + 1)2
d. (3m + 2n)(3m – 2n)
e. (3 – a)(5 + a)
f. (2 + a)(a2 – 2a + 1)
Penyelesaian:
a. (x + 2)(x – 3) = x(x – 3) + 2(x – 3)
= x2 – 3x + 2x – 6
= x2 – x – 6
b. (2x – 3)(x + 4) = 2x(x + 4) – 3(x + 4)
= 2x2 + 8x – 3x – 12
= 2x2 + 5x – 12
c. (4k + 1)2 = (4k + 1)(4k + 1)
= 4k(4k + 1) + 1(4k + 1)
= 16k2 + 4k + 4k + 1
= 16k2 + 8k + 1
d. (3m + 2n)(3m – 2n) = 3m(3m – 2n) + 2n(3m – 2n)
= 9m2 – 6mn + 6mn – 4n2
= 9m2 – 4n2
e. (3 – a)(5 + a) = 3(5 + a) – a(5 + a)
= 15 + 3a – 5a – a2
= 15 – 2a – a2
f. (2 + a)(a2 – 2a + 1) = 2(a2 – 2a + 1) + a(a2 – 2a + 1)
= 2a2 – 4a + 2 + a3 – 2a2 + a
= a3 + 2a2 – 2a2 – 4a + a + 2
= a3 – 3a + 2

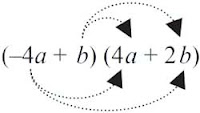
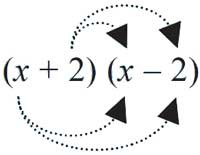
0 Response to "Operasi Hitung Perkalian Bentuk Aljabar, Teladan Soal Dan Pembahasan (Materi Smp)"