Untuk menjumlahkan dan mengurangkan pecahan biasa, terlebih dahulu menyamakan penyebutnya. Penyebut yang sama sebaiknya merupakan KPK dari penyebut-penyebut pecahan yang akan dijumlahkan atau dikurangkan. Lalu bagaimana cara menjumlahkan atau mengurangkan pecahan-pecahan yang berbentuk bilangan desimal?
Nah, pada kesempatan kali ini kita akan mempelajari 2 operasi hitung pada pecahan desimal yang terdiri atas penjumlahan dan pengurangan. Untuk itu, silahkan kalian simak baik-baik klarifikasi berikut ini. Selamat berguru biar dapat paham.
Penjumlahan dan Pengurangan Pecahan Desimal
Pada penjumlahan atau pengurangan bilangan-bilangan dalam bentuk desimal yang perlu diperhatikan ialah lajur-lajur perseratusan, persepuluhan, satuan, puluhan, ratusan, dan sebagainya. Perseratusan ditempatkan dalam satu lajur, demikian juga persepuluhan, koma desimal, satuan, puluhan, ratusan, dan sebagainya. Perhatikan pola berikut ini.
Contoh 1:
Hitunglah nilai penjumlahan dari:
(a) 12,325 + 8,135
(b) 21,032 + 9,802 + 5,181
Jawab:
(a) Bilangan 12,325 terdiri atas puluhan (angka 1), satuan (angka 2), koma desimal (tanda “,”), persepuluhan (angka 3), perseratusan (angka 2) dan perseribuan (angka 5). Bilangan 8,135 terdiri atas satuan (angka 8), koma desimal (tanda “,”), persepuluhan (angka 1), perseratusan (angka 3) dan perseribuan (angka 5). Untuk menjumlahkannya, elemen-elemen pada kedua bilangan tersebut disusun dalam satu lajur menyerupai berikut ini.
1 | 2 | , | 3 | 2 | 5 | |
8 | , | 1 | 3 | 5 | + | |
2 | 0 | , | 4 | 6 | 0 |
Jadi, 12,325 + 8,135 = 20,460 atau dapat kita tulis 20,46.
(b) Bilangan 21,032 terdiri atas puluhan, satuan, koma desimal, persepuluhan, perseratusan dan perseribuan. Bilangan 9,802 terdiri atas satuan, persepuluhan, perseratusan dan perseribuan. Sedangkan bilangan 5,181 juga terdiri atas satuan, persepuluhan, perseratusan dan perseribuan. Lalu jumlahkan ketiga bilangan desimal tersebut dengan cara menyerupai pada soal 1. (a), yaitu sebagai berikut.
2 | 1 | , | 0 | 3 | 2 | |
9 | , | 8 | 0 | 2 | ||
5 | , | 1 | 8 | 1 | + | |
3 | 6 | , | 0 | 1 | 5 |
Jadi, 21,032 + 9,802 + 5,181 = 36,015.
Contoh 2:
Hitunglah nilai pengurangan dari:
(a) 24,56 – 23,72
(b) 25,56 – 13,5
Jawab:
(a) Bilangan 24,56 dan 23,72 terdiri atas puluhan, satuan, koma desimal, persepuluhan dan perseratusan. Sama menyerupai pada penjumlahan, untuk mengurangkan kedua bilangan tersebut caranya susun masing-masing elemen dalam satu lajur, yaitu sebagai berikut.
2 | 4 | , | 5 | 6 | |
2 | 3 | , | 7 | 2 | − |
0 | , | 8 | 4 |
Jadi, 24,56 – 23,72 = 0,84.
(b) Bilangan 25,56 terdiri atas puluhan, satuan, koma desimal, persepuluhan dan perseratusan. Sedangkan bilangan 13,5 terdiri atas puluhan, satuan, koma desimal dan persepuluhan. Agar elemen pada bilangan 13,5 sama dengan elemen pada bilangan 25,56 maka kita dapat menambahkan angka nol dibagian paling belakang angka 13,5 sehingga menjadi 13,50. Untuk mengurangkannya sama menyerupai soal 2. (a) yaitu sebagai berikut.
2 | 5 | , | 5 | 6 | |
1 | 3 | , | 5 | 0 | − |
1 | 2 | , | 0 | 6 |
Jadi, 25,56 – 13,5 = 12,06.
Tips: |
Untuk menjumlahkan atau mengurangkan pecahan desimal dengan cara bersusun ialah jumlahkan atau kurangkan dari kolom yang ada disebelah kanan dan seterusnya hingga kolom yang ada di sebelah kiri. Untuk meletakkan tanda koma juga harus satu garis vertikal. |
Agar pemahaman kalian lebih mantab lagi ihwal konsep penjumlahan dan pengurangan bilangan-bilangan desimal, silahkan kalian simak beberapa pola soal dan pembahasannya berikut ini.
Contoh Soal 1:
Hitunglah nilai penjumlahan dari:
18,05; 56,185, dan 125,2
Jawab:
Bilangan 125,2 mempunyai elemen seribuan, sehingga untuk mempermudah perhitungan, bilangan tersebut diletakkan paling atas. Dengan cara bersusun, maka penjumlahan ketiga bilangan di atas ialah sebagai berikut.
1 | 2 | 5 | , | 2 | 0 | 0 | |
1 | 8 | , | 0 | 5 | 0 | ||
5 | 6 | , | 1 | 8 | 5 | + | |
1 | 9 | 9 | , | 4 | 3 | 5 |
Jadi, 125,2 + 18,05 + 56,185 = 199,435.
Contoh Soal 2:
Hitunglah hasil pengurangan dari:
125,8 – 98,847
Jawab:
Bilangan 125,8 di belakang koma hanya memuat persepuluhan, sedangkan bilangan 98,847 di belakang koma memuat persepuluhan, perseratusan, dan perseribuan. Agar bilangan pertama memuat elemen yang sama pada bilangan kedua, maka kita tambahkan dua angkan 0 (nol) di belakang koma, sehingga menjadi 125,800. Dengan cara bersusun, maka selisih kedua bilangan tersebut adalah:
1 | 2 | 5 | , | 8 | 0 | 0 | |
9 | 8 | , | 8 | 4 | 7 | − | |
2 | 6 | , | 9 | 5 | 3 |
Jadi, 125,8 – 98,847 = 26,953.
Contoh Soal 3:
Hitunglah hasil operasi hitungan bilangan-bilangan pecahan desimal berikut ini.
(a) 2,543 + 1,075 – 3,211
(b) 3,106 – 2,058 + 0,115
Jawab:
(a) Karena sifat penjumlahan dan pengurangan sama-sama kuat, maka pertama kita jumlahkan bilangan 2,543 dengan 1,075 alasannya ialah operasi penjumlahan letakknya paling kiri (pertama).
2 | , | 5 | 4 | 3 | |
1 | , | 0 | 7 | 5 | + |
3 | , | 6 | 1 | 8 |
Selanjutnya hasil penjumlahan tersebut kita kurangkan dengan bilangan desimal terakhir yaitu sebagai beriku.
3 | , | 6 | 1 | 8 | |
3 | , | 2 | 1 | 1 | − |
0 | , | 4 | 0 | 7 |
Jadi, 2,543 + 1,075 – 3,211 = 0,407.
(b) Sama menyerupai pada pola soal 3. (a), alasannya ialah operasi pengurangan letaknya paling pertama maka kita selesaikan dahulu operasi pengurangan tersebut, yaitu sebagai berikut.
3 | , | 1 | 0 | 6 | |
2 | , | 0 | 5 | 8 | − |
1 | , | 0 | 4 | 8 |
Lalu hasil selisih tersebut, kita jumlahkan dengan bilangan ketiga, yaitu sebagai berikut.
1 | , | 0 | 4 | 8 | |
0 | , | 1 | 1 | 5 | + |
1 | , | 1 | 6 | 3 |
Jadi, 3,106 – 2,058 + 0,115 = 1,163
Contoh Soal Cerita:
Dua buah kapal bahari berangkat dari salah satu pelabuhan dengan jalur yang sama. Kapal pertama berangkat dari pelabuhan pada pagi hari dan kapal kedua berangkat dari pelabuhan pada sore harinya. Pada hari kedua, jarak yang ditempuh kapal pertama sejauh 356,175 km sedangkan kapal kedua sejauh 218,25 km. Tentukanlah selisih jarak yang ditempuh kapal pertama dan kapal kedua!
Jawab:
Misalkan kapal pertama = A, dan kapal kedua = B
Jarak yang ditempuh kapal A = 356,175 km
Jarak yang ditempuh kapal B = 218,25 km
Maka, selisih jarak antara kapal A dan kapal B ialah sebagai berikut.
3 | 5 | 6 | , | 1 | 7 | 5 | |
2 | 1 | 8 | , | 2 | 5 | − | |
1 | 3 | 7 | , | 9 | 2 | 5 |
Dengan demikian, selisih jarak antara kapal pertama dan kedua ialah 147,925 km.
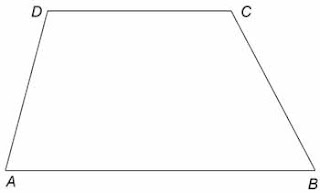
Contoh Soal Geometri:
Diketahui:
AB = 18,2 cm, AD = 13,8 cm, dan CD = 12,5 cm.
Jika keliling trapesium ABCD ialah 59,8 cm, tentukanlah panjang sisi BC!
Jawab:
Keliling trapesium ialah jumlah keempat sisinya yaitu sebagai berikut.
⇒ Keliling = AB + AD + CD + BC
⇒ 59,8 = 18,2 + 13,8 + 12,5 + BC
⇒ 59,8 = 44,5 + BC
⇒ BC = 59,8 – 44,5
⇒ BC = 15,3
Jadi, panjang sisi BC ialah 15,3 cm.

0 Response to "Penjumlahan & Pengurangan Kepingan Desimal, Pola Soal Dan Pembahasan (Materi Smp)"