Pada kesempatan kali ini kita akan membahas wacana operasi hitung bentuk aljabar yang terdiri atas penjumlahan, pengurangan, perkalian, pembagian, dan perpangkatan lengkap dengan pola soal dan pembahasan. Untuk itu, silahkan kalian simak baik-baik klarifikasi berikut ini.
Operasi Hitung Penjumlahan dan Pengurangan Bentuk Aljabar
Sifat-sifat penjumlahan dan pengurangan pada bilangan bundar juga berlaku pada bentuk aljabar tetapi operasi penjumlahan dan pengurangan pada bentuk aljabar hanya sanggup dilakukan pada suku-suku yang sejenis saja.
Perhatikan bentuk aljabar berikut ini.
3a + 5b + 3c + 2a + 7c – 3b
Aljabar di atas sanggup dinyatakan dalam bentuk yang lebih sederhana dengan cara mengelompokkan suku-suku yang sejenis sampai diperoleh bentuk ibarat berikut ini.
3a + 5b + 3c + 2a + 7c – 3b = (3a + 2a) + (5b – 3b) + (3c + 7c)
⇒ 5a + 2b + 10c
Untuk menuntaskan penjumlahan atau pengurangan suku-suku sejenis dari bentuk aljabar sanggup dilakukan dengan cara mengelompokkan dan menyusun ke bawah. Untuk lebih jelasnya, perhatikan pola berikut ini.
Contoh:
1. Sederhanakan bentuk-bentuk aljabar di bawah ini.
a. 2a + 4b + 3a
b. 3x + 6y + 14x – 8y
Penyelesaian:
a. 2a + 4b + 3a = 2a + 3a + 4b = (2 + 3)a + 4b = 5a + 4b
b. 3x + 6y + 14x – 8y = 3x + 14x + 6y – 8y = (3 + 14)x + (6 – 8)y = 17x – 2y
2. Jumlahkan 3a + 5b + 7c dengan 4b + 5a + 3c dengan cara:
a. mengelompokkan, dan
b. menyusun ke bawah.
Penyelesaian:
a. Cara mengelompokkan
⇒ (3a + 5b + 7c) + (4b + 5a + 3c)
⇒ (3a + 5a) + (5b + 4b) + (7c + 3c)
⇒ (3 + 5) a + (5 + 4) b + (7 + 3)c
⇒ 8a + 9b + 10c
b. Cara menyusun ke bawah
3a + 5b + 7c | |
5a + 4b + 3c | + |
8a + 9b + 10c |
3. Kurangkan 2a + 5b – 3c dengan a + 3b + 2c dengan cara:
a. mengelompokkan, dan
b. menyusun ke bawah.
Penyelesaian:
a. Cara mengelompokkan
⇒ (2a + 5b – 3c) – (a + 3b + 2c)
⇒ 2a + 5b – 3c – a – 3b – 2c
⇒ (2a – a) + (5b – 3b) + (–3c – 2c)
⇒ (2 – 1) a + (5 – 3) b + (–3 – 2) c
⇒ a + 2b + (–5) c
⇒ a + 2b – 5c
b. Cara menyusun ke bawah
2a + 5b – 3c | |
a + 3b + 2c | – |
a + 2b – 5c |
Operasi Hitung Perkalian Bentuk Aljabar
Operasi hitung perkalian pada bentuk aljabar ada dua bentuk, yakni perkalian antara konstanta dengan bentuk aljabar dan perkalian antara dua bentuk aljabar. Berikut klarifikasi beserta contoh-contoh soalnya.
1. Perkalian antara konstanta dengan bentuk aljabar
Perkalian suatu bilangan konstanta k dengan bentuk aljabar suku satu dan suku dua dinyatakan sebagai berikut.
k(ax) = kax k(ax + b) = kax + kb |
Contoh:
Jabarkan bentuk aljabar berikut ini, kemudian sederhanakanlah.
a. 4(p + q)
b. 5(ax + by)
c. 3(x – 2) + 6(7x + 1)
d. -8(2x – y + 3z)
Penyelesaian:
a. 4(p + q) = 4p + 4q
b. 5(ax + by) = 5ax + 5by
c. 3(x – 2) + 6(7x + 1) = 3x – 6 + 42x + 6
= 3x + 42x – 6 + 6
= (3 + 42)x + 0
= 45x
d. -8(2x – y + 3z) = -16x + 8y – 24z
2. Perkalian antara dua bentuk aljabar
Sebagaimana perkalian suatu konstanta dengan bentuk aljabar, untuk memilih hasil kali antara dua bentuk aljabar kita sanggup memanfaatkan sifat distributif perkalian terhadap penjumlahan dan sifat distributif perkalian terhadap pengurangan.
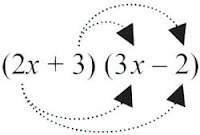
Selain dengan cara tersebut, untuk memilih hasil kali antara dua bentuk aljabar, sanggup memakai cara sebagai berikut. Perhatikan perkalian antara bentuk aljabar suku dua dengan suku dua berikut.
Selain dengan cara denah ibarat di atas, untuk mengalikan bentuk aljabar suku dua dengan suku dua sanggup dipakai sifat distributif ibarat uraian berikut ini.
(ax + b)(cx + d) = ax(cx + d) + b(cx + d)
= ax × cx + ax × d + b × cx + b × d
= acx2 + adx + bcx + bd
= acx2 + (ad + bc)x + bd
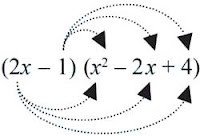
Adapun pada perkalian bentuk aljabar suku dua dengan suku tiga berlaku sebagai berikut.
= ax × cx2 + ax × dx + ax × e + b × cx2 + b × dx + b × e
= acx3 + adx2 + aex + bcx2 + bdx + be
= acx3 + (ad + bc)x2 + (ae + bd)x + be
Contoh:
Tentukan hasil perkalian bentuk aljabar berikut dalam bentuk jumlah atau selisih.
1. (2x + 3)(3x – 2)
2. (–4a + b)(4a + 2b)
3. (2x – 1)(x2 – 2x + 4)
4. (x + 2)(x – 2)
Penyelesaian:
1. (2x + 3)(3x – 2) kita selesaian dengan dua cara, yakni sebagai berikut.
● Cara (1) dengan sifat distributif
(2x + 3)(3x – 2) = 2x(3x – 2) + 3(3x – 2)
= 6x2 – 4x + 9x – 6
= 6x2 + 5x – 6
● Cara (2) dengan skema
= 2x × 3x + 2x × (–2) + 3 × 3x + 3 × (–2)
= 6x2 – 4x + 9x – 6
= 6x2 + 5x – 6
2. (–4a + b)(4a + 2b) kita selesaikan dengan dua cara, yakni sebagai berikut.
● Cara (1) dengan sifat distributif
(–4a + b)(4a + 2b) = –4a(4a + 2b) + b(4a + 2b)
= –16a2 – 8ab + 4ab + 2b2
= –16a2 – 4ab + 2b2
● Cara (2) dengan skema
= (–4a) × 4a + (–4a) × 2b + b × 4a + b × 2b
= –16a2 – 8ab + 4ab + 2b2
= –16a2 – 4ab + 2b2
3. (2x – 1)(x2 – 2x + 4) kita selesaikan dengan dua cara, yakni sebagai berikut.
● Cara (1) dengan sifat distributif
(2x – 1) (x2 – 2x + 4) = 2x(x2 – 2x + 4) – 1(x2 – 2x + 4)
= 2x3 – 4x2 + 8x – x2 + 2x – 4
= 2x3 – 4x2 – x2 + 8x + 2x – 4
= 2x3 – 5x2 + 10x – 4
● Cara (2) dengan skema
= 2x × x2 + 2x × (–2x) + 2x × 4 + (–1) × x2 + (– 1) × (–2x) + (–1) × 4
= 2x3 – 4x2 + 8x – x2 + 2x – 4
= 2x3 – 4x2 – x2 + 8x + 2x – 4
= 2x3 – 5x2 + 10x – 4
4. (x + 2)(x – 2) kita selesaikan dengan dua cara, yakni sebagai berikut.
● Cara (1) dengan sifat distributif
(x + 2)(x – 2) = x(x – 2) + 2(x – 2)
= x2 – 2x + 2x – 4
= x2 – 4
● Cara (2) dengan skema
= x × x + x × (–2) + 2 × x + 2 × (–2)
= x2 – 2x + 2x – 4
= x2 – 4
Operasi Hitung Pembagian Bentuk Aljabar
Hasil bagi dua bentuk aljabar sanggup kalian peroleh dengan memilih terlebih dahulu faktor sekutu masing-masing bentuk aljabar tersebut, kemudian melaksanakan pembagian pada pembilang dan penyebutnya. Untuk lebih jelasnya, perhatikan pola berikut ini.
Contoh:
Sederhanakanlah pembagian bentuk aljabar berikut ini.
1. 3xy : 2y
2. 6a3b2 : 3a2b
3. x3y : ( x2y2 : xy)
4. (24p2q + 18pq2) : 3pq
Penyelesaian:
1. | 3xy : 2y | = | 3xy |
2y |
= | 3 | x | (faktor sekutu y) |
2 |
2. | 6a3b2 : 3a2b | = | 6a3b2 |
3a2b |
= | 3a2b × 2ab | (faktor sekutu 3a2b |
3a2b |
= 2ab
3. | x3y : ( x2y2 : xy) | = | x3y | : | x2y2 | ||
xy |
= | x3y | : | xy × xy | ||
xy |
= | x3y : xy | = | xy × x2 |
xy |
= x2
4. | (24p2q + 18pq2) : 3pq | = | 24p2q + 18pq2 |
3pq |
= | 6pq(4p + 3q) |
3pq |
= 2(4p + 3q)
Operasi Hitung Perpangkatan Bentuk Aljabar
Coba kalian ingat kembali bahan wacana operasi perpangkatan pada bilangan bulat. Operasi perpangkatan diartikan sebagai bentuk perkalian berulang dengan bilangan yang sama. Jadi, untuk sebarang bilangan bundar a, berlaku sebagai berikut.
pn | = | p × p × p × … × p |
sebanyak n faktor |
Hal ini juga berlaku pada perpangkatan bentuk aljabar. Untuk lebih jelasnya, perhatikan pola berikut ini.
Contoh Soal 1:
Tentukan hasil perpangkatan bentuk aljabar berikut.
1. (2p)2
2. –(3x2yz3)3
3. (–3p2q)2
Penyelesaian:
1. (2p)2 = (2p) × (2p) = 4p2
2. –(3x2yz3)3 = –27x6y3z9
3. (–3p2q)2 = 9p4q2
Contoh Soal 2:
a. (2a)2
b. (3xy)3
c. (–2ab)4
d. (4a2b2)2
e. –3(x2y)3
f. –(2pq)4
g. 1/2(2xy)2
h. a(ab2)3
Penyelesaian:
a. (2a)2 = 4a2
b. (3xy)3 = 9x3y3
c. (–2ab)4 = 16a4b4
d. (4a2b2)2 = 16a4b4
e. –3(x2y)3 = -3(x5y3) = -3x5y3
f. –(2pq)4 = -(16p4q4) = -16p4q4
g. 1/2(2xy)2 = 1/2(4x2y2) = 2x2y2
h. a(ab2)3 = a(a3b5) = a4b5
Pada perpangkatan bentuk aljabar suku dua, koefisien tiap suku ditentukan menurut segitiga Pascal. Misalkan kita akan memilih pola koefisien pada pembagian terstruktur mengenai bentuk aljabar suku dua (a + b)n, dengan n bilangan asli. Perhatikan uraian berikut.
□ (a + b)1 = a + b → koefisiennya 1 1
□ (a + b)2 = (a + b)(a + b)
= a2 + ab + ab+ b2
= a2 + 2ab+ b2 → koefisiennya 1 2 1
□ (a + b)3 = (a + b)(a + b)2
= (a + b)(a2 + 2ab + b2)
= a3 + 2a2b + ab2 + a2b + 2ab2 + b3
= a3 + 3a2b + 3ab2 + b3 → koefisiennya 1 3 3 1
dan seterusnya.
Adapun pangkat dari a (unsur pertama) pada (a + b)n dimulai dari an kemudian berkurang satu demi satu dan terakhir a1 pada suku ke-n. Sebaliknya, pangkat dari b (unsur kedua) dimulai dengan b1 pada suku ke-2
lalu bertambah satu demi satu dan terakhir bn pada suku ke-(n + 1).
Perhatikan pola koefisien yang terbentuk dari pembagian terstruktur mengenai bentuk aljabar (a + b)n di atas. Pola koefisien tersebut ditentukan berdasarkan segitiga Pascal berikut.
Pada segitiga Pascal tersebut, bilangan yang berada di bawahnya diperoleh dari penjumlahan bilangan yang berdekatan yang berada di atasnya.
Sekarang perhatikan pola berikut ini.
Contoh Soal 3:
Jabarkan bentuk aljabar berikut.
a. (3x + 5)2
b. (2x – 3y)2
c. (x + 3 y)3
d. (a – 4)4
Penyelesaian:
a. (3x + 5)2 = 1(3x)2(5)0 + 2(3x)1(5)1 + 1(3x)0(5)2
= 1(9x2)(1) + 2(3x)(5) + 1(1)(25)
= 9x2 + 30x + 25
b. (2x – 3y)2 = 1(2x)2(-3y)0 + 2(2x)1(–3y)1 + 1(2x)0(–3y)2
= 1(4x2)(1) + 2(2x)(–3y) + 1(1)(9y2)
= 4x2 – 12xy + 9y2
c. (x + 3y)3 = 1(x)3(3y)0 + 3(x)2(3y)1 + 3(x)1(3y)2 + 1(x)0(3y)3
= 1(x3)(1) + 3(x2)(3y) + 3(x)(9y2) + 1(1)(27y3)
= x3 + 9x2y + 27xy2 + 27y3
d. (a – 4)4 = 1(a)4(-4)0 + 4(a)3(-4)1 + 6(a)2(-4)2 + 4(a)1(-4)3 + 1(a)0(-4)4
= 1(a4)(1) + 4(a3)(-4) + 6(a2)(16) + 4(a)(-64) + 1(1)(256)
= a4 − 16a3 + 96a2 − 256a + 256




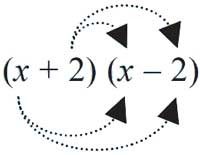

0 Response to "Operasi Aljabar: Penjumlahan, Pengurangan, Perkalian, Pembagian & Perpangkatan (Materi Smp)"