Contoh Soal Penyederhanaan Bentuk Aljabar Dan Pembahasannya Lengkap (Materi Smp)

Pernahkah kau sakit batuk? Apa yang kau lakukan? Apakah kau ke dokter? Bila kau memeriksakan diri atau berobat ke dokter biasanya dokter akan menunjukkan resep. Contoh obat yang dibeli dengan resep dokter:

Pada botol Vitamin C tertulis sehari 3 × 1. Pada botol obat batuk tertulis sehari 3 × 2 sendok teh.

Apa arti “3 × 1” atau “3 × 2” itu?

Vitamin C 3 × 1 artinya dalam sehari vitamin C harus diminum 3 kali, sekali minum 1 tablet. Dengan perkataan lain dalam sehari banyaknya vitamin C yang harus diminum yaitu 3, yaitu 1 + 1 + 1. Sehingga 3 × 1 artinya 1 + 1 + 1.

Obat batuk 3 × 2 sendok teh artinya dalam sehari obat batuk harus diminum 3 kali, sekali minum 2 sendok teh. Dengan perkataan lain dalam sehari banyaknya obat batuk yang harus diminum yaitu 6 sendok teh, yaitu dari 2 + 2 + 2. Sehingga 3 × 2 artinya 2 + 2 + 2.

Arti dari hukum pemakaian obat di atas sebetulnya sama dengan arti perkalian dalam matematika.

“3 × 1” atau “3 × 2” sanggup diartikan sebagai berikut.

3 × 1 = 1 + 1 + 1

3 × 2 = 2 + 2 + 2

Bilangan-bilangan dalam tanda kotak sanggup diganti dengan lambang sebarang Asli, contohnya a. Sehingga jika diganti dengan aksara a, maka:

1 × a ditulis a

2 × a atau ditulis 2a, dan 2a = a + a

3 × a atau ditulis 3a, dan 3a = a + a + a

4 × a atau ditulis 4a, dan 4a = a + a + a + a

Dan seterusnya.

Perhatikan. 1 × a ditulis a

Perhatikan resep dokter “obat batuk sehari 2 × 2 - sendok teh”. Dalam matematika, perkalian untuk bilangan yang sama, menyerupai “2 × 2” itu sanggup ditulis 22. Apakah pada obat yang dibeli dengan resep dokter sanggup ditulis 22? Jawabannya tidak dapat. Mengapa? Coba jelaskan.

Selanjutnya pada matematika,

2 × 2 × 2 sanggup ditulis 23.

2 × 2 × 2 × 2 × 2 sanggup ditulis 25, dan seterusnya.

Penulisan itu berlaku juga untuk sebarang bilangan bulat, misalkan a. Dengan demikian berlaku hal berikut.

a4 = a × a × a × a

a5 = a × a × a × a × a, dan seterusnya.

Perhatikan. a1 ditulis a

Perhatikan lagi aksara a dalam 2a, 3a atau a2. Huruf a tersebut dinamakan variabel, sedang 2a, 3a atau a2 disebut bentuk aljabar. Contoh bentuk-bentuk aljabar dengan variabel a yaitu 3a2 + a, -2a. Contoh bentuk-bentuk aljabar dengan variabel b yaitu b2 + 4, 3b + 5 dan sebagainya. Contoh bentuk-bentuk aljabar dengan variabel a dan b yaitu b2 + a, 3b + 5a dan sebagainya.

Contoh Soal 1

Sederhanakan penulisannya.

a) 3a2 + 4a2

b) -2b3 + 4b3

c) 9a – 13a

Penyelesaian:

a) 3a2 + 4a2 = (a2 + a2 + a2) + (a2 + a2 + a2 + a2) = 7a2

atau dengan sifat distributif perkalian terhadap penjumlahan.

3a2 + 4a2 = (3 + 4)a2 = 7a2.

Untuk selanjutnya, kita pakai sifat distributif perkalian terhadap penjumlahan untuk menjumlahkan bentuk aljabar itu.

b) –2b3 + 4b3 = (–2 + 4)b3 = 2b3

c) 9a – 13a = (9 – 13)a = -4a

Contoh Soal 2

Sederhanakan bentuk aljabar 5a3 + 4a2 – a2 + 9a + 6

Penyelesaian:

Bentuk aljabar 5a3 + 4a2 – a2 + 9a + 6 sanggup disederhanakan juga dengan mengumpulkan dan menjumlahkan atau mengurangkan suku-suku sejenis.

5a3 + 4a2 – a2 + 9a + 6 = 5a3 + (4 – 1) a2 + 9a + 6

⇒ 5a3 + 3a2 + 9a + 6

Bentuk yang terakhir ini terdiri dari 4 suku, yaitu 5a3, 3a2, 9a dan 6.

Contoh Soal 3

Sederhanakan bentuk aljabar berikut.

a) 3x4 + 2x2 + x – 2

b) 6s3 + 2s2 – 3s2 + s – 5

Penyelesaian:

a) Bentuk aljabar ini tidak sanggup disederhanakan lagi, alasannya yaitu tidak mempunyai suku-suku yang sejenis.

b) 6s3 + 2s2 – 3s2 + s – 5 = 6s3 + (2 – 3)s2 + s – 5

⇒ 6s3 + (–1)s2 + s – 5

⇒ 6s3 – s2 + s – 5

Bentuk aljabar kadangkala memakai “perkalian” antara variabel dengan lambang bilangan bulat. Sehingga untuk menyederhanakannya kita memakai sifat distributif perkalian terhadap penjumlahan atau terhadap pengurangan. Untuk lebih jelasnya perhatikan referensi berikut.

Contoh Soal 4

Gunakan sifat distributif perkalian terhadap penjumlahan atau terhadap pengurangan untuk menyederhanakan soal-soal di bawah ini.

a) 5(a + 2b)

b) 7(2x – 5)

c)	25a + 35b
	5

d) (2a)3

Penyelesaian:

a) 5(a + 2b) = (5 × a) + (5 × 2b)

⇒ 5a + 10b

b) 7(2x – 5) = 7(2x) + 7(-5)

⇒ 14x – 35

c)	25a + 35b	=	25a	+	35b
	5		5		5

⇒ 5a + 7b

d) (2a)3 = 2a × 2a × 2a

⇒ (2 × 2 × 2) × (a × a × a)

⇒ 23 × a3

⇒ 23a3

Contoh Soal 5

Sederhanakan bentuk aljabar di bawah ini.

a) 2x – 5y + 6x – 2y

b) 4a – 3b – 5a + 2b

Penyelesaian:

a) 2x – 5y + 6x – 2y = 2x + 6x – 5y – 2y

⇒ (2 + 6) x + (–5 – 2)y

⇒ 8x + (–7)y = 8x – 7y

b) 4a – 3b – 5a + 2b = 4a – 5a – 3b + 2b

⇒ (4 – 5)a + (–3 + 2)b

⇒ (–1)a + (–1)b

⇒ –a – b

Perhatikan bahwa bentuk-bentuk aljabar selalu memuat satu atau lebih dari satu variabel. Variabel itu sanggup diganti dengan sebarang bilangan bulat. Pada soal sering terdapat perintah untuk mengganti atau substitusi suatu variabel dengan bilangan tertentu. Bagaimana mendapat hasilnya? Perhatikan referensi berikut.

Contoh Soal 6

Jika p = 2, q = 3 dan r = 6, carilah hasil dari:

a) p + q

b) p + q + 2r

c) 3p2 – 2r

Penyelesaian:

a) p + q = 2 + 3 = 5

b) p + q + 2r = 2 + 3 + 2(6) = 2 + 3 + 12 = 17

c) 3p2 – 2r = 3(2)2 – 2(6) = 3(4) – 12 = 12 – 12 = 0

Contoh Soal 7

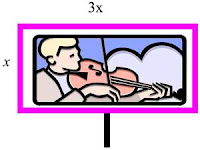
Papan nama perusahaan, hotel-hotel atau tempat-tempat hiburan pada umumnya berbentuk suatu persegipanjang. Bila panjang dan lebar suatu papan nama yaitu 3x meter dan x meter. Berapakah keliling papan nama itu?

Penyelesaian:

Misalkan keliling papan nama = K meter, maka:

K = 2(panjang + lebar)

K = 2(3x + x)

⇒ 2(3x) + 2(x)

⇒ 6x + 2x = 8x

Jadi keliling papan nama itu yaitu 8x meter.